Peer springt im Quadrat

Im Rätsel "Gartenzwerge" sind ja schon Angela und Guido vertreten.
Guido spielt nicht mehr mit, dafür bekommt Peer jetzt dieses Rätsel.

Die Seitenlänge g des großen Quadrates ist 5 mal so groß wie die Seitenlänge k jedes der kleinen quadratischen Felder. Peer springt nun von jedem Feld zu einem benachbarten; so besucht er alle Felder, jedes aber nur ein einziges Mal.
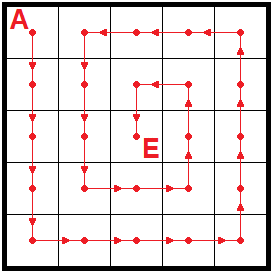
Er beginnt ganz links oben im Feld A und springt immer linksherum in Pfeilrichtung.
Vor dem Feld A muss er wieder nach unten, denn auf A war er ja schon.
So springt er weiter, bis er zum Schluss im Feld E angekommen ist.
Nun hat er alle Felder besucht und setzt sich zur Ruhe.
Wieviele Sprünge hat er insgesamt gemacht?

Wir fassen Sprünge in gleicher Richtung zusammen: 4↓, 4→, 4↑, 3←, 3↓, 2→, 2↑, 1←, 1↓, das sind insgesamt 3·4 + 2·3 + 2·2 + 2·1 = 4 + 2·(4 + 3 + 2 + 1).
Der letzte Ausdruck erinnert uns an die Gaußsche Summenformel (s. z.B. Rätsel "Kartenhaus").
Mit der finden wir vielleicht auch die Zahl der Sprünge, wenn die Seitenlänge des großen Quadrates z.B. 27- oder allgemein n-mal (mit beliebiger positiver ganzer Zahl n) so groß ist wie die jedes der kleinen Felder.
Probieren wir's aus!

Oder geht alles sogar noch leichter?
Lösung anzeigen